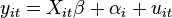Menghitung validitas data ordinal atau data interval dapat dilakukan dengan menggunakan SPSS karena sudah tersedia di menu utama. Sedangkan untuk data numerik, tidak ada menu spss yang khusus menyediakan perhitungan validitas dengan rumus point biserial ini. Kita dapat melakukannya dengan menambahkan syntax khusus pada SPSS.
Berikut syntax yang harus di save di spss:
langhah1: Buka SPSS
langkah 2: buka File –> New –> Syntax–> kemudian save di directory D komputer anda dengan nama file: “r_bis”.
syntax pertama:
/* —————————————————– */
/* SPSS-Macro r_bis */
/* */
/* (Version 2.1; D. Enzmann, 2002) */
/* */
/* r_bis computes the biserial correlation of a dicho- */
/* tomous variable with a continuous variable and its */
/* significance. The biserial correlation computed is */
/* restricted to upper and lower bounds of 1.0 and -1.0, */
/* respectively. */
/* */
/* The dichotomous variable need not to be coded as 0/1. */
/* If one of the variable is a constant or if both */
/* variables have more than two valid categories r_bis */
/* will issue an error message. If both variables are */
/* dichotomous, r_bis may produce meaningless results */
/* (a tetrachoric correlation coefficient should be */
/* computed, instead). */
/* */
/* If the number of cases is more than 12,0000 you have */
/* to increase the default value of MXLOOPS to the */
/* the number of cases in your current working file */
/* after you installed the macro via INCLUDE. */
/* */
/* Example: */
/* One variable x is coded ‘1’ for ‘no/false’ and ‘2’ */
/* for ‘yes/true’, the other variable y is continuous. */
/* Your data file consists of about 22800 cases. First, */
/* use the SET MXLOOP command once to increase the */
/* default value of 12000 to at least 22800: */
/* SET MXLOOP=23000. */
/* Next, you can call r_bis with x and y as parameters */
/* r_bis x y . */
/* */
/* A full example can be found in the file EXAMP_R.SPS . */
/* */
/* —————————————————– */.
set printback on
/mxloops=120000.
PRESERVE.
set printback off.
define r_bis ( !positional !tokens(1)
/!positional !tokens(1))
matrix.
get raw
/file=*
/variables=!1 !2
/names = vname
/missing omit.
compute tmpvars=make(1,5,0).
compute errmsg={‘ ‘}.
compute minmaxx=0.
compute minmaxy=0.
compute min=mmin(raw(:,1)).
compute max=mmax(raw(:,1)).
compute x0=0.
compute x1=0.
loop #i=1 to nrow(raw).
do if (raw(#i,1)=min).
+ compute x0=x0+1.
else if (raw(#i,1)=max).
+ compute x1=x1+1.
end if.
end loop.
compute xn = x0+x1.
do if min=max.
+ compute minmaxx=1.
end if.
compute min=mmin(raw(:,2)).
compute max=mmax(raw(:,2)).
compute tmpvars(1,1) = nrow(raw).
compute y0=0.
compute y1=0.
loop #i=1 to nrow(raw).
do if (raw(#i,2)=min).
+ compute y0=y0+1.
else if (raw(#i,2)=max).
+ compute y1=y1+1.
end if.
end loop.
compute yn = y0+y1.
do if min=max.
+ compute minmaxy=1.
end if.
do if yn=tmpvars(1,1).
+ compute tmpvars(1,2)=y0.
+ compute tmpvars(1,3)=y1.
else if xn=tmpvars(1,1).
+ compute tmpvars(1,2)=x0.
+ compute tmpvars(1,3)=x1.
end if.
do if minmaxx or minmaxy.
+ compute tmpvars(1,2)=0.
+ compute tmpvars(1,3)=0.
end if.
do if (xn=yn).
+ compute tmpvars(1,5)=1.
end if.
do if (tmpvars(1,2) > 0) and (tmpvars(1,3) > 0)
and not(minmaxx or minmaxy).
+ compute SSCPMat=SSCP(raw-(make(tmpvars(1,1),1,1))
*csum(raw)/tmpvars(1,1)).
+ compute tmpvars(1,4) = SSCPMat(1,2)/sqrt(SSCPMat(1,1)*SSCPMat(2,2)).
+ compute probn0n = tmpvars(1,2)/tmpvars(1,1).
/* compute idfnormal(n0/n,0,1) */
/* ALGORITHM AS241 APPL. STATIST. (1988) VOL. 37, NO. 3 */
/* */
/* Produces the normal deviate Z corresponding to a given lower */
/* tail area of P; Z is accurate to about 1 part in 10**16. */.
compute SPLIT1 = 0.425.
compute SPLIT2 = 5.
compute CONST1 = 0.180625.
compute CONST2 = 1.6.
/* Coefficients for P close to 0.5 */
compute A = {3.3871328727963666080,
1.3314166789178437745E+2,
1.9715909503065514427E+3,
1.3731693765509461125E+4,
4.5921953931549871457E+4,
6.7265770927008700853E+4,
3.3430575583588128105E+4,
2.5090809287301226727E+3}.
compute B = {1.0,
4.2313330701600911252E+1,
6.8718700749205790830E+2,
5.3941960214247511077E+3,
2.1213794301586595867E+4,
3.9307895800092710610E+4,
2.8729085735721942674E+4,
5.2264952788528545610E+3}.
/* Coefficients for P not close to 0, 0.5 or 1 */
compute C = {1.42343711074968357734,
4.63033784615654529590,
5.76949722146069140550,
3.64784832476320460504,
1.27045825245236838258,
2.41780725177450611770E-1,
2.27238449892691845833E-2,
7.74545014278341407640E-4}.
compute D = {1.0,
2.05319162663775882187,
1.67638483018380384940,
6.89767334985100004550E-1,
1.48103976427480074590E-1,
1.51986665636164571966E-2,
5.47593808499534494600E-4,
1.05075007164441684324E-9}.
/* Coefficients for P near 0 or 1 */
compute E = {6.65790464350110377720,
5.46378491116411436990,
1.78482653991729133580,
2.96560571828504891230E-1,
2.65321895265761230930E-2,
1.24266094738807843860E-3,
2.71155556874348757815E-5,
2.01033439929228813265E-7}.
compute F = {1.0,
5.99832206555887937690E-1,
1.36929880922735805310E-1,
1.48753612908506148525E-2,
7.86869131145613259100E-4,
1.84631831751005468180E-5,
1.42151175831644588870E-7,
2.04426310338993978564E-15}.
compute zpn0n=-7.9414444931916800.
do if probn0n <= 10E-16.
+ compute probn0n = 10E-16.
else if 1-probn0n <= 10E-16.
+ compute probn0n = 1 – 10E-16.
end if.
compute exitf=0.
compute ifault = 0.
compute q = probn0n – 0.5.
do If (Abs(q) <= SPLIT1).
+ compute r = CONST1-q*q.
* compute zpn0n = q*(((((((A7*r+A6)*r+A5)*r+A4)*r+A3)*r+A2)*r+A1)*r+A0).
* compute zpn0n = zpn0n/(((((((B7*r+B6)*r+B5)*r+B4)*r+B3)*r+B2)*r+B1)*r+1).
+ compute t1=A(8).
+ compute t2=B(8).
+ loop #i=-7 to -1.
– compute t1=r*t1+A(-#i).
– compute t2=r*t2+B(-#i).
+ end loop.
+ compute zpn0n=q*t1/t2.
/* Exit Function */
+ compute exitf=1.
end if.
do If (q < 0) and not exitf.
+ compute r = probn0n.
Else if not exitf.
+ compute r = 1 – probn0n.
End If.
do If (r <= 0) and not exitf.
+ compute ifault = 1.
+ compute zpn0n = 0.
/* Return */
End If.
do if not exitf.
+ compute r = sqrt(-ln(r)).
end if.
do If (r <= SPLIT2) and not exitf.
+ compute r = r – CONST2.
* compute zpn0n = (((((((C7*r+c6)*r+c5)*r+c4)*r+c3)*r+c2)*r+c1)*r+C0).
* compute zpn0n = zpn0n/(((((((D7*r+D6)*r+d5)*r+d4)*r+d3)*r+d2)*r+d1)*r+1).
+ compute t1=C(8).
+ compute t2=D(8).
+ loop #i=-7 to -1.
– compute t1=r*t1+C(-#i).
– compute t2=r*t2+D(-#i).
+ end loop.
+ compute zpn0n=t1/t2.
Else if not exitf.
+ compute r = r – SPLIT2.
* compute zpn0n = (((((((E7*r+E6)*r+E5)*r+E4)*r+E3)*r+E2)*r+E1)*r+E0).
* compute zpn0n = zpn0n/(((((((F7*r+F6)*r+F5)*r+F4)*r+F3)*r+F2)*r+F1)*r+1).
+ compute t1=E(8).
+ compute t2=F(8).
+ loop #i=-7 to -1.
– compute t1=r*t1+E(-#i).
– compute t2=r*t2+F(-#i).
+ end loop.
+ compute zpn0n=t1/t2.
End If.
do If (q < 0) and not exitf.
+ compute zpn0n = -zpn0n.
End If.
release a, b, c, d, e, f.
* ——————————————— .
+ COMPUTE d = EXP(-.5 * zpn0n**2)/sqrt(8*artan(1)).
+ compute rb = sqrt(tmpvars(1,2)*tmpvars(1,3))*tmpvars(1,4)/
(d*tmpvars(1,1)).
+ do if rb > 1.0.
– compute rb = 1.0.
+ end if.
+ do if rb < -1.0.
– compute rb = -1.0.
+ end if.
+ compute sigm_rb=sqrt(tmpvars(1,2)*tmpvars(1,3))/
(d*tmpvars(1,1)*sqrt(tmpvars(1,1))).
+ compute z = rb/sigm_rb.
+ compute p = (1-cdfnorm(abs(z)))*2.
+ print {vname(1),’ with ‘,vname(2)}
/title ‘Biseral correlation:’
/format A8.
+ print {tmpvars(1,1),rb,p}
/title ‘ ‘
/clabels = ‘N’,’r’,’p(2-sided)’
/formats F13.5.
+ do if tmpvars(1,5)=1.
– print errmsg
/title ‘> warning: both variables are dichotomous’
/format A1.
+ end if.
else if (tmpvars(1,2)=0) and (tmpvars(1,3)=0)
and not(minmaxx or minmaxy).
+ print {vname(1),’ with ‘,vname(2)}
/title ‘Biseral correlation:’
/format A8.
+ print {tmpvars(1,1)}
/title ‘ ‘
/rlabels = ‘N = ‘
/formats F8.0.
+ print errmsg
/title ‘> error: there is no dichotomous variable’
/format A1.
else.
+ print {vname(1),’ with ‘,vname(2)}
/title ‘Biseral correlation:’
/format A8.
+ print {tmpvars(1,1)}
/title ‘ ‘
/rlabels = ‘N = ‘
/formats F8.0.
+ print errmsg
/title ‘> error: at least one variable is a constant’
/format A1.
end if.
end matrix.
!enddefine.
restore.
/* ———————————————- */.
/* r_bis is called by: */.
/* */.
/* R_BIS var1 var2. */.
/* */.
/* Remember to set the MXLOOP setting to the */.
/* number of cases in your data file the first */.
/* time you call R_BIS by using */.
/* SET MXLOOP=nnn. */.
/* (with nnn >= number of cases) */.
/* ———————————————- */.
Langkah Ketiga: buka File –> New –> Syntax–> kemudian save di directory komputer anda.
syntax kedua:
include ‘d:\r_bis.sps’.
/* Dibawah ini anda sedang menghitung KORELASI BISERIAL item-total */
/* Nama variabel di SPSS harus disesuaikan dengan nama di syntax */
/* a1,a2 dst untuk nama variabel dan tot untuk nama total */
/* anda bisa menambahkan aitem sesuai dengan jumlah aitem alat ukur anda */
r_bis item1 total.
r_bis item2 total.
r_bis item3 total.
r_bis item4 total.
r_bis item5 total.
r_bis item6 total.
r_bis item7 total.
r_bis item8 total.
r_bis item9 total.
r_bis item10 total.
r_bis item11 total.
r_bis item12 total.
r_bis item13 total.
r_bis item14 total.
r_bis item15 total.
r_bis item16 total.
r_bis item17 total.
r_bis item18 total.
r_bis item19 total.
r_bis item20 total.
/* Dibawah ini anda sedang menghitung KORELASI POINT BISERIAL item-total */
/* Nama variabel di SPSS harus disesuaikan dengan nama di syntax */
/* a1,a2 dst untuk nama variabel dan tot untuk nama total */
/* anda bisa menambahkan aitem sesuai dengan jumlah aitem alat ukur anda */
corr item1 total.
corr item2 total.
corr item3 total.
corr item4 total.
corr item5 total.
corr item6 total.
corr item7 total.
corr item8 total.
corr item9 total.
corr item10 total.
corr item11 total.
corr item12 total.
corr item13 total.
corr item14 total.
corr item15 total.
corr item16 total.
corr item17 total.
corr item18 total.
corr item19 total.
corr item20 total.